Bloom Filters

Bloom filters

Bloom filters are space-efficient, probabilistic data structures that quickly check if an element might be in a set, offering a trade-off: they can tell you if an item is "definitely not in the set" or "possibly in the set," but never "definitely in the set" (allowing for false positives but no false negatives).

Essentially it is an array of N bits with K hash functions. In our day to day lives, bloom filters act as first line of defense to ensure unnecessary db queries are not made and time is saved.

• Imagine Instagram,
  • you are creating an account on for the Meta Platform., who already have billions of users -> 8 billion usernames.
  • Ideally, if the entire accounts data was sorted lexicographically in a balanced tree it would take us 33 steps to get the result of whether a username is taken or not.
    • This is feasible but still expensive in terms of memory locality, cache misses, and disk access at scale.
  • Now that we know the data is not sorted, we have linear search, but that would be painfully slow. it would take hours before your username is said to be available for you.
  • What if we could get our result in constant time. Yes CONSTANT, irrelevant of the size of the dataset we have. Bloom filters help us do that

How do Bloom Filters work?

• At its core, a Bloom filter is just a bit array of size N, initially all set to 0.
• Along with this array, we choose K independent hash functions.
  • Each hash function maps an input (like a username) to one position in the bit array.
• When inserting an item (say, a new username):
  • The username is passed through all K hash functions.
  • Each hash function returns an index between 0 and N-1.
  • The bits at all those indices are set to 1.
  • No actual usernames are stored — only the bits are updated.
• When querying an item (checking if a username exists):
  • The username is hashed using the same K hash functions.
  • We check the corresponding K bit positions in the array.
    • If any one of them is 0 → the username is definitely not in the set.
    • If all of them are 1 → the username is possibly in the set.
• This is what gives Bloom filters their guarantee:
  • No false negatives — if the filter says “not present,” it’s always correct.
  • False positives are possible — bits may have been set by other usernames.
• The lookup cost is:
  • O(K) operations
  • Since K is a small constant, this is effectively constant time, independent of how many usernames exist.
• In practice:
  • A Bloom filter acts as a gatekeeper.
  • If it says “definitely not present,” the system skips the database entirely.
  • If it says “possibly present,” the system performs a definitive database lookup.
• The result:
  • Fewer unnecessary DB queries
  • Lower latency
  • Better cache locality
  • Predictable performance at massive scale

False Positives?

• Yes, in order to optimize the space and results, we make this one gamble. False positives.
• An example of this would be you searching up a username you desire but it says already taken, you make an account and search for the same username and there is no user with this id.
• Could this be a hurdle causing too many false positives, not allowing you to select an id you desire?

The MATH

But how many false positives is too many? Won't this become a hiccup? Let's get slightly mathematical here

Let's set our bases here - A false positive occurs when all k hash positions are already set to 1. - A false positive means the result says an item is "possibly in the set", even though the value is not present in the set. - We have a N targets here, that is N sized bitmap array - We have K hash functions - We have m items - Thus in total we will be doing k*m throws - k hash function runs for m items - Now let's run the math here, skip to XX if you don't want the math I understand :( -
To calculate probability of false positive
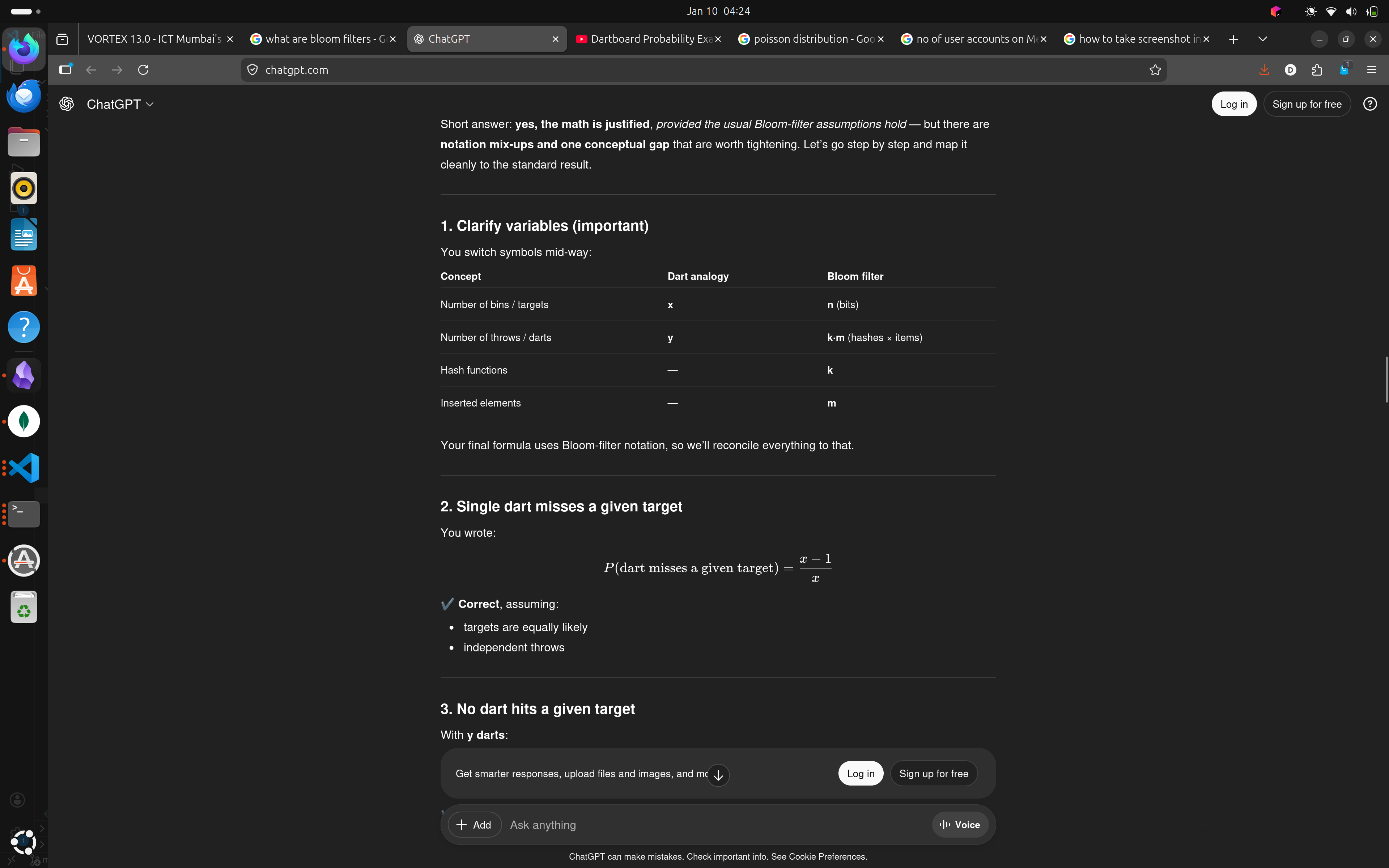
- Example -> Throwing darts | x targets | y darts
- \(P\)(given dart will not hit a given target) = \((x-1)/x\)
- \(P\)(not of the \(y\) darts hit a given target) = \(((x-1)/x)^y\)
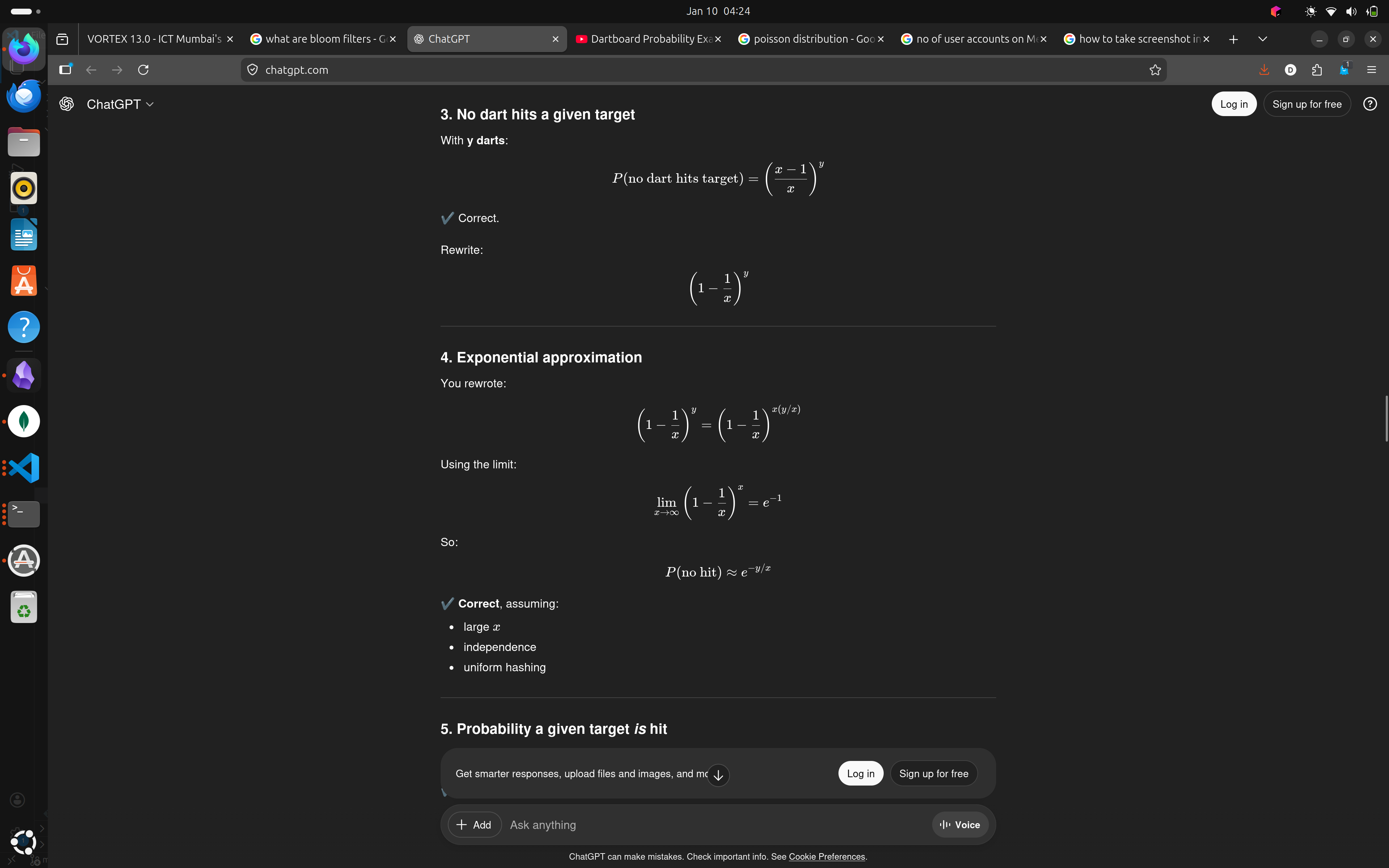
- The above equation can be written as $\((1-1/x)^{x(\frac{y}{x})}\)$
- approximation -> \((1 - \epsilon)^{1/\epsilon} \ = \ 1/e\)
- Thus, we conclude, P(no darts hit a given target) = \(e^{-y/x}\)
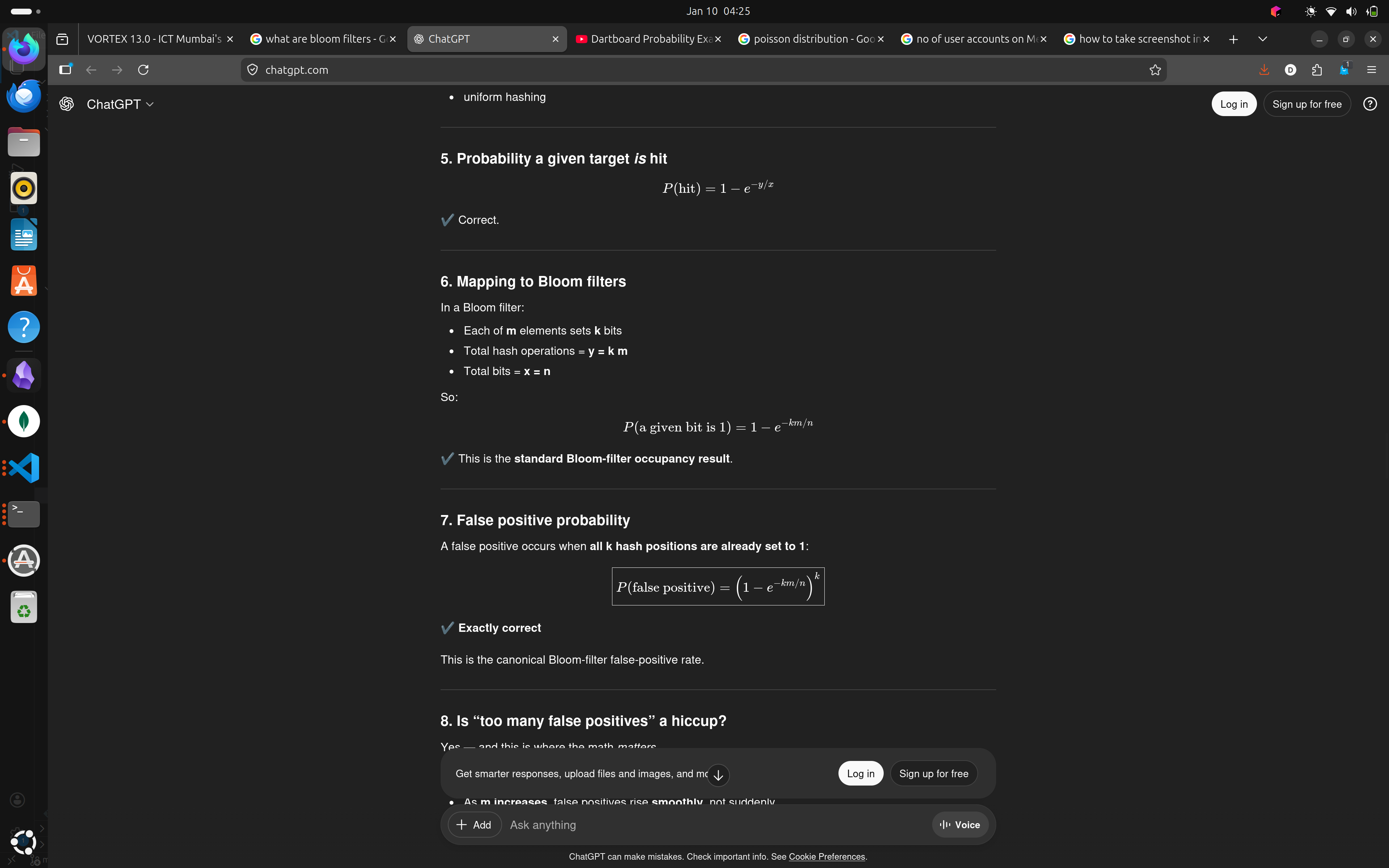
- and, P(a given target is hit) = 1 - \(e^{-y/x}\)
- False Positive rate = $\((1-e^{-km/n})^k\)$Where
- k -> number of hash functions - m-> number of set members - n -> total number of bits

I do not remember calculus as well, this was me researching at 4am in the morning because I couldn't understand shit.