Cryptographic Algorithms

Symmetric Key Algorithms¶

Substitution Cipher¶

letters/plaintext replaced by other letters/numbers/symbols

Pigpen Cipher¶

letter substitution
Alphabets are arranged as follows:

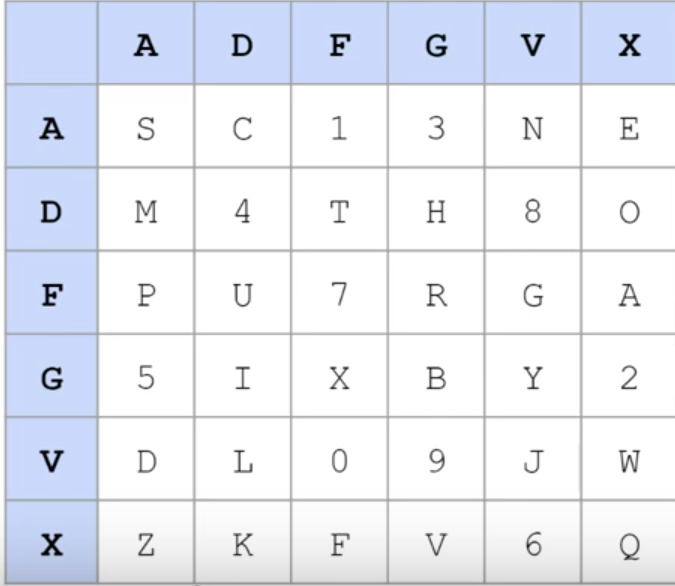
ADFGVX Cipher¶

It Exhibits
- Confusion $\rightarrow$ each char goes through substitution via a key to create cipher text
- Fractionation $\rightarrow$ each character in plain text becomes 2 characters in cipher text
- Diffusion $\rightarrow$ 2 paired cipher-text characters in the cipher-text are spread into different parts of the final cipher-text message
Uses a Polybius square (6x6 matrix with 26 letters and 10 digits)
Steps (ENCRYPTION)
1. Substituition text generation
  - Replace each character in the plain text with row-character``column-character for the plain text occurrence in the Polybius square.
    - each letter or number substitute the letter pair fromthe column and row heading
  - M $\rightarrow$ DA ; H $\rightarrow$DG ; Q $\rightarrow$ XX
2. Creating cipher text from diffusion character
  - Choose a keyword with no repeated characters(IMP!!) in the keyword
  - Create a table using every character from keyword as a column.
  - Input the substitution text generated in last step into this new table in row-wise manner
  - Sort the Columns in lexicographical ( alphabetical ) order, read each column to generate cipher text
Steps (DECRYPTION)
- Given: Ciphertext and keyword
- Create the table using sorted keyword columns and place the ciphertext in the table in column wise order (top->bottom for each column then next column)
- Re-arrange the table by moving columns to match the keyword
- Read text row-wise in the table (You got the substitution text)
- Break down into chunks of two characters and reverse find replacements in the Polybius square.
Why $ADFGVX$ characters specifically? Because these had dissimilar patterns in morse code.

Caesar Cipher¶

Replace each letter by 3rd letter after it
\[CipherText\ = E(p) = (p+k)\ mod\ 26$$$$PlainText = D(c) = (c-k) \ mod \ 26\]
Easy to decipher by brute-forcing through different k values
Do need to recognise when we have the plain text though

Affine Cipher¶

Encryption $\(c \Rightarrow E(p) = \alpha p + \beta \ Mod \ 26$\)
Decryption $\(p \Rightarrow D(c) = \alpha^{-1}(c-\beta)$\)
$\alpha\ and\ \beta$ must be selected such that $gcd(\alpha,\beta)$ = $1$
- i.e. $\alpha$ and $\beta$ must be co-prime

Monoalphabetic Cipher¶

Don't shift the alphabet, shuffle the letters arbitrarily
Map the newly shuffled alphabets to the a-z alphabet scheme
- each plain-text letter maps to a different random cipher-text letter
CONS
- Frequency distribution can break this down easily

Playfair Cipher¶

Rules
- No repeating letters in the keyword
Steps (Table generation 5x5)
- Remove letter j from the alphabet.
- Your selected keyword would go at the start of the 5x5 matrix
  - keyword cannot have repeating characters
- Fill in the remaining blocks with remaining characters from alphabet missing in keyword in increasing order (i.e. a,b...z) [except j]
Steps for preparing Message
- Split letters in pairs of two
- Separate all duplicated letters by putting X in between
  - MESSAGE $\rightarrow$ ME SX SA GE
- Insert each pair into the table and IF the pair characters:
  - are in same column
    - Move each letter down ONE (Wrap around at last)
  - are in same row
    - Move each letter right ONE (Wrap around at last)
  - forms a rectangle
    - Swap letters with the opposite corners (same row swap after imagining the rectangle.)
Decryption:
- Reverse the above steps
- Same column $\rightarrow$ Move each letter up by one
- Same row $\rightarrow$ Move each letter left by one
- rectangle $\rightarrow$ swap adjacent corners

Hill Cipher¶

Polygraphic substitution cipher
Each letter treated as digit in base 26
Ciphertext = Key * Plaintext
Uses Linear Algebra
Pre-requisites
- Matrix Multiplication
- Inverse of a Matrix Calculation
- Modulo 26
Encryption
- use formula $E(K,P) = K*P$
  - k and P are matrices
  - If the column size are row size does not match? We break plain text into parts and merge later.
Decryption
- Find inverse of matrix $K$ in mod 26.
- $P=D(K,C) = K^{-1} * C$
- $K^{-1}$ has two steps
  - Finding Determinant of the matrix
  - Finding Adjacent of the matrix
    - 2x2 matrix
      - swap $M_{1,1}\ and \ M_{2,2}$
      - swap sign for $M_{1,2} \ and \ M_{2,1}$
    - 3x3 matrix
The secret key matrix K should be chosen carefully and needs to fulfill that $K * K^{-1} = Identity\ in\ MOD\ 26$
Can be broken by a cipher text attack.

Vignere Cipher¶

Vignere Square
- 26 rows x 26 columns [a-z][a-z]
- Each row of the table corresponds to caesar cipher (an kth shift of the alphabet)
  - 0 shifts in the first row, n-1 shifts in the nth row.
ENCRYPTION -> $E_i\ = \ (P_i\ + K_i)\ mod\ 26$
- To encrypt the message, write the key, followed by plain text below the key so that the letters are aligned.
  - The key is repeated till it match plain text in length
- The Cipher text is generated using the Vigenere square.
  - Key Letters $\rightarrow$ indicate the row
  - plain text Letters $\rightarrow$ indicate the column
  - Find intersection of each letter using row and column to get the character to substitute it with.
- Do this for all letters, you got the cipher text
**DECRYPTION $D_i\ = \ (P_i\ - K_i)\ mod\ 26$ **
- Write letters of the KEY, followed by the CIPHER Text
- Plain Text Generation (using letters of):
  - Cipher text $\rightarrow$ select row
  - Key $\rightarrow$ select Column
- VigenereSquare[cipherText[i]][key[i]]$_i$ = $plaintext_i$
Cryptanalysis
- Secure from attack using frequency Analysis; not a completely secure cipher
- If attacker finds the length of the key, can be broken using
- Plaintext attack is possible against this cipher

One Time Pad¶

The key length has to be as long as the length of the plain text
Encryption
- $C_i=P_i \oplus K_i$
Decryption
- $P_i=C_i \oplus K_i$
Drawback $\rightarrow$ large key size

Transposition Cipher¶

aka permutation ciphers (hide message by rearranging letter orders) without altering actual letters used
The letters are written in a row under the key and then column arranged as per alphabetical order.
Two types
- Single columnar
- Double columnar

Single Columnar - Row transposition Cipher¶

Read the key, and number the letters of the key as per their appearance in the alphabet.
Encryption divided into 3 parts:
1. Preparing the key
2. Preparing plain text
3. Encryption
Key Preparation:
- Each letter in the key gets a value based on alphabetical ordering
- If a letter is repeated the ordering is done from left to right
  - eea -> e2,e3,a1
Plain text prep:
- Letters from the message are written in rows under the numbered letters of the key.
- This forms a table with len(key) columns
Encryption
- Rearrange the table in the ascending ordering of the column key values that were assigned at the beginning
- Copy the letters column wise from top to bottom
Decryption
- Create an empty table with columns for keyword-characters.
- Number the characters based on alphabetic order and left-right precedence
- Fill thee cypher text in columns from top to bottom in the keyword's increasing order of assigned values to characters.
For any blank spaces fill in dummy character, 'X' is preferred due to overall lower frequency

Double Columnar Transposition¶

We do the #Single Columnar - Row transposition Cipher, just twice.
We may use the same key, or use two different keys to create cipher text by doing the Encryption step twice
For decrypting do the reverse, in reverse order of keys.

Questions: 1. What is a plaintext attack exactly? What is Cipher text attack?