Data Streams
Stream Data Model
- Any number of streams can enter the system
- Each stream can provide elements at its own schedule.
- No requirement of having same data rates or data types.
- Streams can be huge in size, and thus may be archived in a large archival storage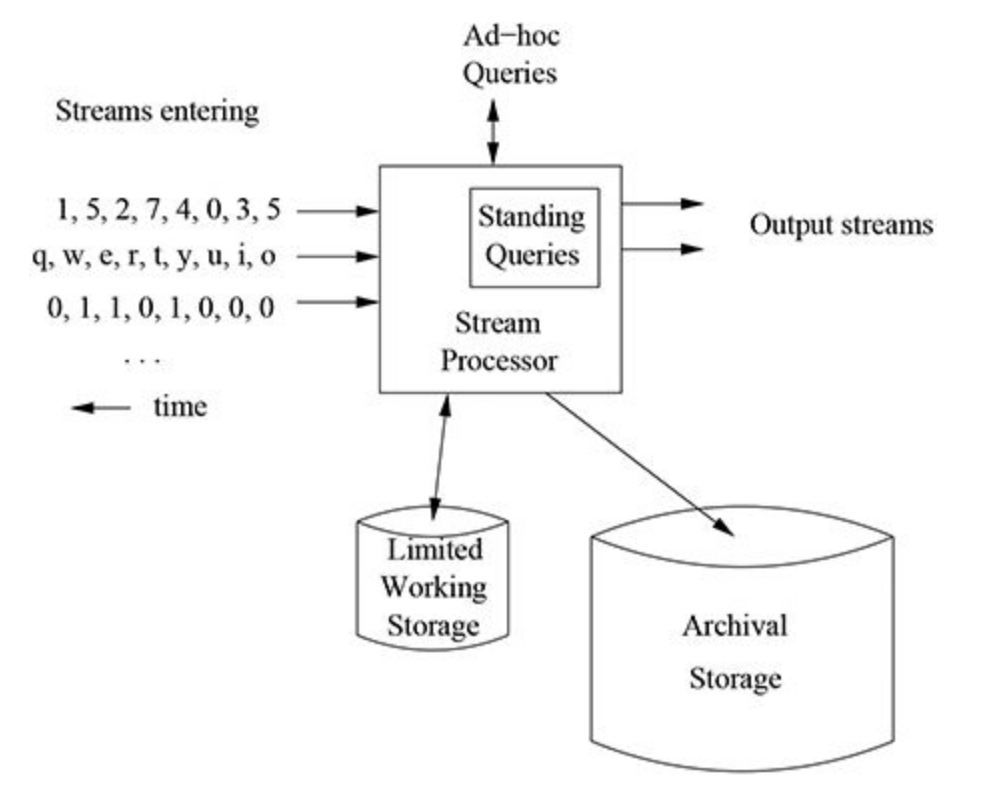 - Working store -> summaries of parts of streams are placed. Queries can be run here
- Working store -> summaries of parts of streams are placed. Queries can be run here
Stream Sources
- Sensor Data
- Image Data
- Internet and Web Traffic
Stream Queries
- Standing queries are permanently executing queries and produce outputs at appropriate times
- Example, to output an alert whenever the temperature exceeds 25\(\degree\) centigrade.
- Ad-hoc queries is a question asked once about the current state of a stream(s)
- common approach is to store a sliding window of each stream in the working store
Issues in Stream Processing
- Given enough memory, many problems in streaming data would be very easy to solve
- It is much more efficient to get an approximate answer to our problem than exact solution
- Hashing techniques can be used to produce approximate answer
Sampling Data in Stream
¶
- selecting a subset of a stream so that we can ask queries about the selected subset and have the answers be statistically representative of the stream as a whole.
- We assume the stream consists of tuples (user, query, time) – of which only user is in the key.
Filtering Streams
- Another common process on streams is selection, or filtering.
-
Bloom Filtering
- It is a way to check whether the element \(\omega\) is present in the set \(S\).
- We cannot remove an item from the 04:00bloom filter, it never forgets
- Uses the main memory as a bit array.
Bloom filter consists of:- An array of n bits, initially all set to 0
- Collection of hash functions \(h_1, h_2,...h_k\), each function maps 'key' values to n buckets.
- set S of m key values.
- An array of n bits, initially all set to 0
Purpose -> Allow through all stream elements whose keys are in \(S\), rejecting most of the stream elements whose keys are not in \(S\).-
How to check- Begin with all bits set to 0
- Take each key value in \(S\) and hash it using each of the \(k\) hash functions, update each bit at the \(h_i(K_j)\) to 1. ... \(h_i(Key_j)\) -> return value from hash function
- To test a key arriving in stream, check that all of \(h_1(K),h_2(K),..h_k(K)\) are 1s in the bit array.
- If all are 1's then it is a probable yes. If even a single bit turns out 0 then it's a definite NO.
- Begin with all bits set to 0
-
To calculate probability of false positive- Example -> Throwing darts | x targets | y darts
- \(P\)(given dart will not hit a given target) = \((x-1)/x\)
- \(P\)(not of the \(y\) darts hit a given target) = \(((x-1)/x)^y\)
- The above equation can be written as $\((1-1/x)^{x(\frac{y}{x})}\)$
- approximation -> \((1 - \epsilon)^{1/\epsilon} \ = \ 1/e\)
- Thus, we conclude, P(no darts hit a given target) = \(e^{-y/x}\)
- and, P(a given target is hit) = 1 - \(e^{-y/x}\)
- The above equation can be written as $\((1-1/x)^{x(\frac{y}{x})}\)$
- False Positive rate = $\((1-e^{-km/n})^k\)$Where
- k -> number of hash functions
- m-> number of set members
- n -> total number of bits
- Example -> Throwing darts | x targets | y darts