Decision Tree

  • used for classification and predicting
  • Two steps
    • Entropy
    • Information Gain
  • How to find Root Node?
    • Calculate Entropy for all the given attributes
    • Choose the one with the highest information gain.
  • Entropy
    • \[Entropy = \sum_{i=1}^n -p_i*log_2(p_i)\]
  • Information Gain:
    \(\(Gain(S,A) = Entropy(S) - \sum_{v \ \epsilon D_A} \frac{|S_V|}{|S|}Entropy(S_V)\)\)


Methods for expressing Test Conditions
- Depends on attribute types - Binary - Nominal - Ordinal - Continuous - Split types - Multi Way Split - Use as many partitions as distinct values - Binary Split - Divides values into two subsets


Measures of Node Impurity
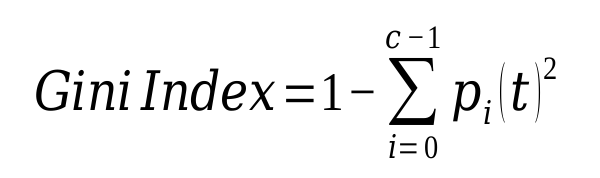
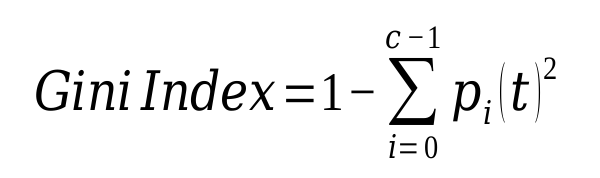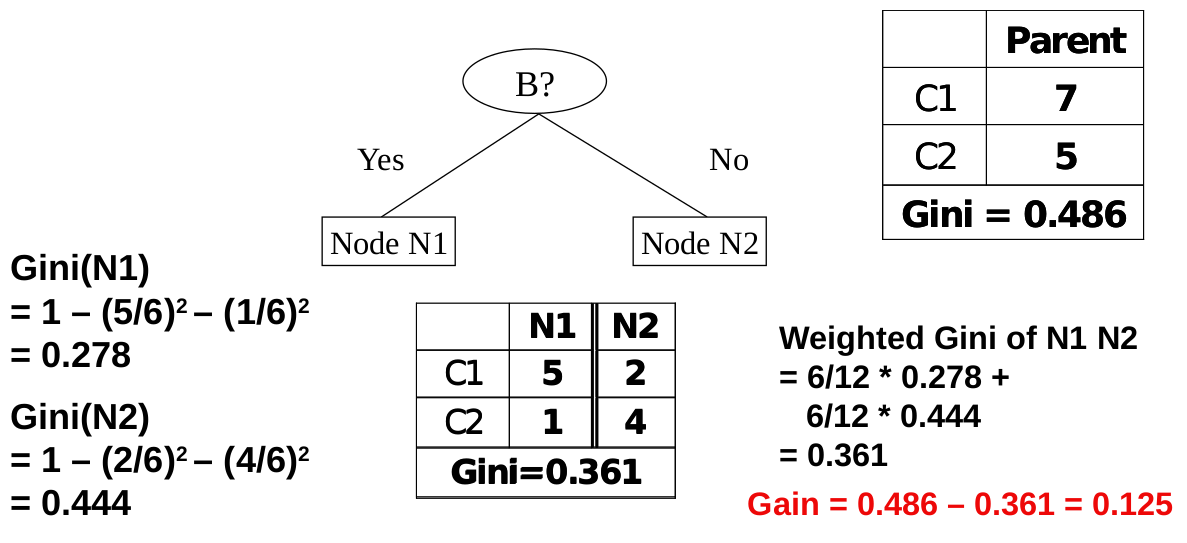
- giniIndex.pngginiIndex.png - - For 2-class problem (p, 1 – p) ; GINI = 1 – p2 – (1 – p)2 = 2p (1-p) - Pasted image 20240501225651.png


Gain Ratio
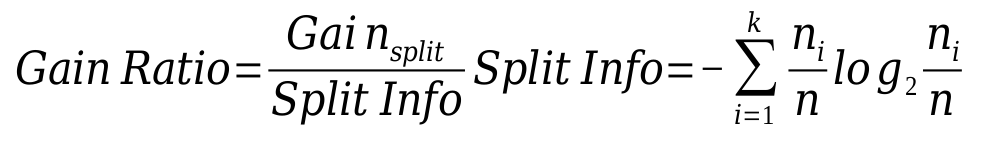
- Gain Ratio.png


Computing Error of a Single Node
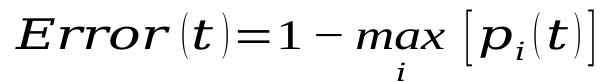- errorInASingleNode.png - In simple words, Error(t) i.e. Classification Error is equal to 1 - max probability of all values - E.g.Pasted image 20240501231501.png

Advantages: - Relatively inexpensive to construct - Extremely fast at classifying unknown records - Easy to interpret for small-sized trees - Robust to noise (especially when methods to avoid overfitting are employed) - Can easily handle redundant attributes - Can easily handle irrelevant attributes (unless the attributes are interacting)

Disadvantages: - Due to the greedy nature of splitting criterion, interacting attributes (that can distinguish between classes together but not individually) may be passed over in favor of other attributed that are less discriminating. - Each decision boundary involves only a single attribute