Design Techniques–III

Backtracking

N-Queen's Problem (4/8)

• Time Complexity -> O(n!)
• Back tracking approach to find all solutions
• from root node assign all possible values to the queen node in DFS order
• At any point, if row/column/diagonal rule broken, preempt the branch!

Hamiltonian Cycle

• NP Hard Problem
• Exponential time taking problem
• Articulation point -> if present, hamiltonian cycle not possible in graph
  • It is a single point which joins two parts of a graphs via a single point 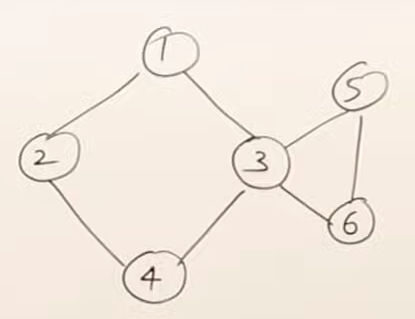3 is the articulation point here!
• Algorithm
  • Initially the array of cycle elements are 0
  • We fix a starting vertex to avoid duplicate cycles
  • choose a vertex from the graph such that it has a edge to the previous node.
• Bounding Function Checks
  • Do not take any duplicates
  • Whenever taking a vertex, there should be an edge from the previous vertex
  • When on the last vertex, there should be an edge to the first vertex
• Complexity:
  • For N nodes, we do n! steps
  • n! = (n * n-1 * n-2 ... *1)
  • which is approximately equal to O(\(n^n\))

Graph Colouring

• Color Vertex here not EDGE! i.e. we assign the colour to the vertex and not the edge.
• Optimisation Problem -> Minimum number of colours required for Colouring the graph
• mColouring Decision Problem -> Given colors, can we color the graph with only these many colours | aka Chromatic Problem
• Base conditions
  • if color matches with adjacent node's color, preempt the branch
• Applications
  • Time table design
  • Map coloring S.T no two connected regions share the same colour
• T.C -> O(\(m^v\)) .. Where m-> Number of colors | v -> Number of Vertex

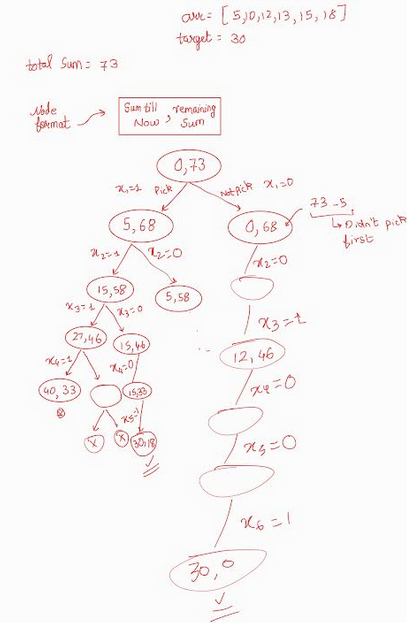
Subset Sum

• Given : input array of numbers , targetValue
• Base conditions:
  1. Sum/weight till now should be less than or equal to targetValue
  2. remaining weight of the array should be greater than or equal to the remaining (targetValue -currentSum )
• Tree constructed as -> Weight Included or Not Included (i.e. 2 children)..

0/1 Knapsack

• use Pick not pick logic to build tree to maximize the profit by choosing the best possible combination for the knapsack problem
• Input -> Array of Profit, Weight for n objects AND knapsack size
• Bounding condition
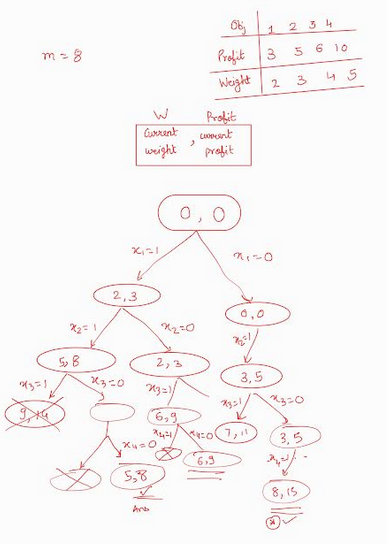
  • current weight should be less than or Equal to our knapsack weight!
• Time Complexity -> O(2^n)

Branch and Bound

• Similar to back tracking -> uses a state space tree as well
• Useful for solving optimzation problems
• We can only solve minimization problems using this

0/1 knapsack problem

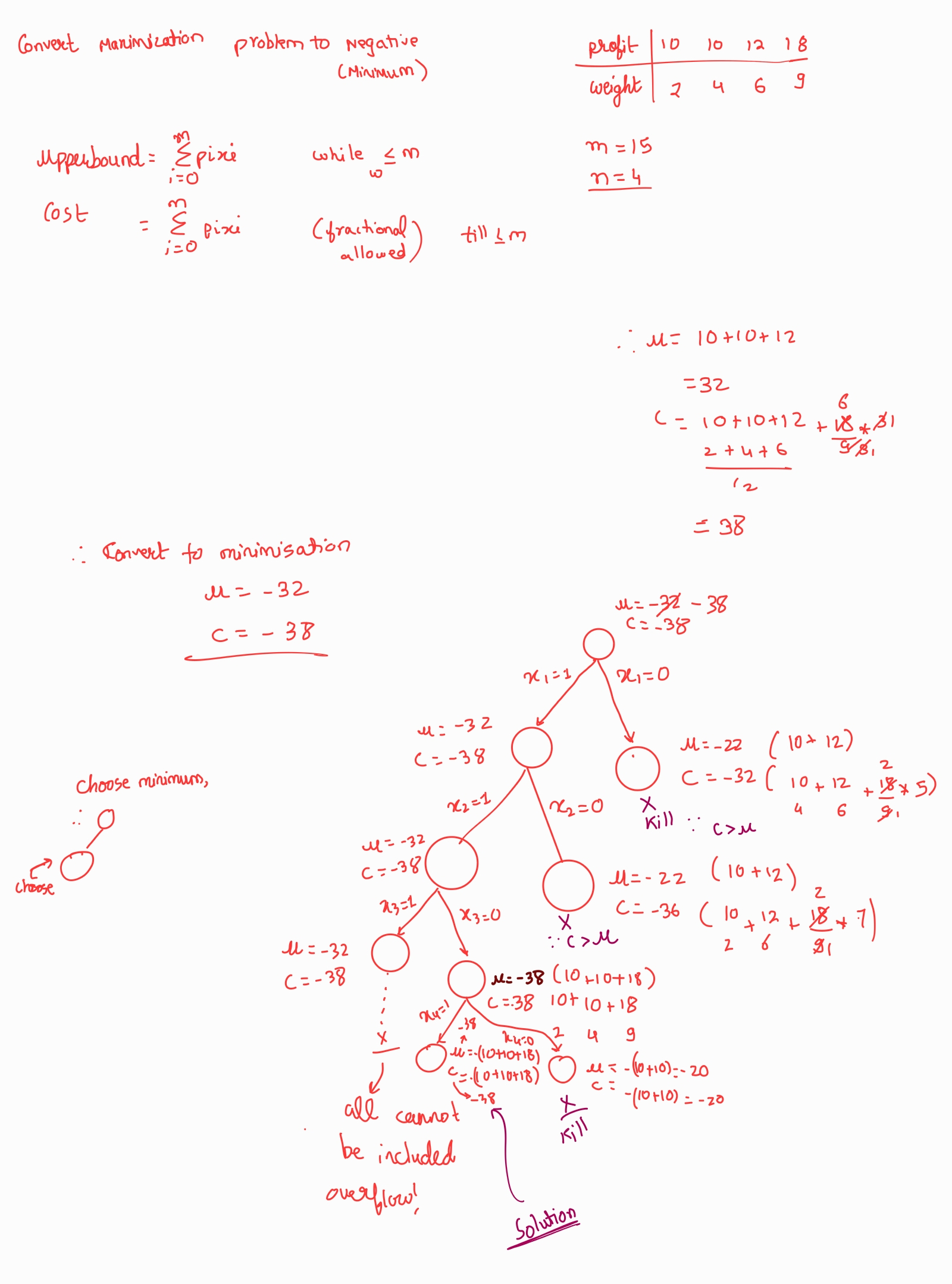
• Maximization problem has to be converted to minimization problem
• Least Cost Branch Bound method used, explore the node with minimum cost
  • upperBound (u) = sum of all the profits till their total weight is less than knapsackSize
  • cost -> sum of all the profits, ( with fractions included) for minimization part and not as part of problem
  • fixed size solution -> {0,1,1,0} | 1-> pick , 0 -> not pick
• If at any point the cost of a node is greater than upper, kKill the node!
• Continue till you have killed all nodes except one which would be the answer node.

Travelling Sales Man Problem

• Update given cost matrix by reducing the matrix M
• In this algorithm when generating tree we travel in level order and not DFS!
• reduce by removing minimum element from each row from the entire row and then the minimum element from each colum from the entire column.
  • cost of the first matrix is the reduced cost i.e. here 25
  • When going from vertex 1 to 2, make the first row and second column as \(\infty\) , similarly, we wouldn't want to go back to 1 from 2 again, so update 2,1 to \(\infty\) .
  • cost of vertex -> cost of edge from previous to current +cost of previous vertex+ current reduction cost
  • In the next iteration, we have to make all previous values from current vertex to infinity to avoid going back to ancestor vertex
  • of all the leaves, pick the one with the least cost
  • 
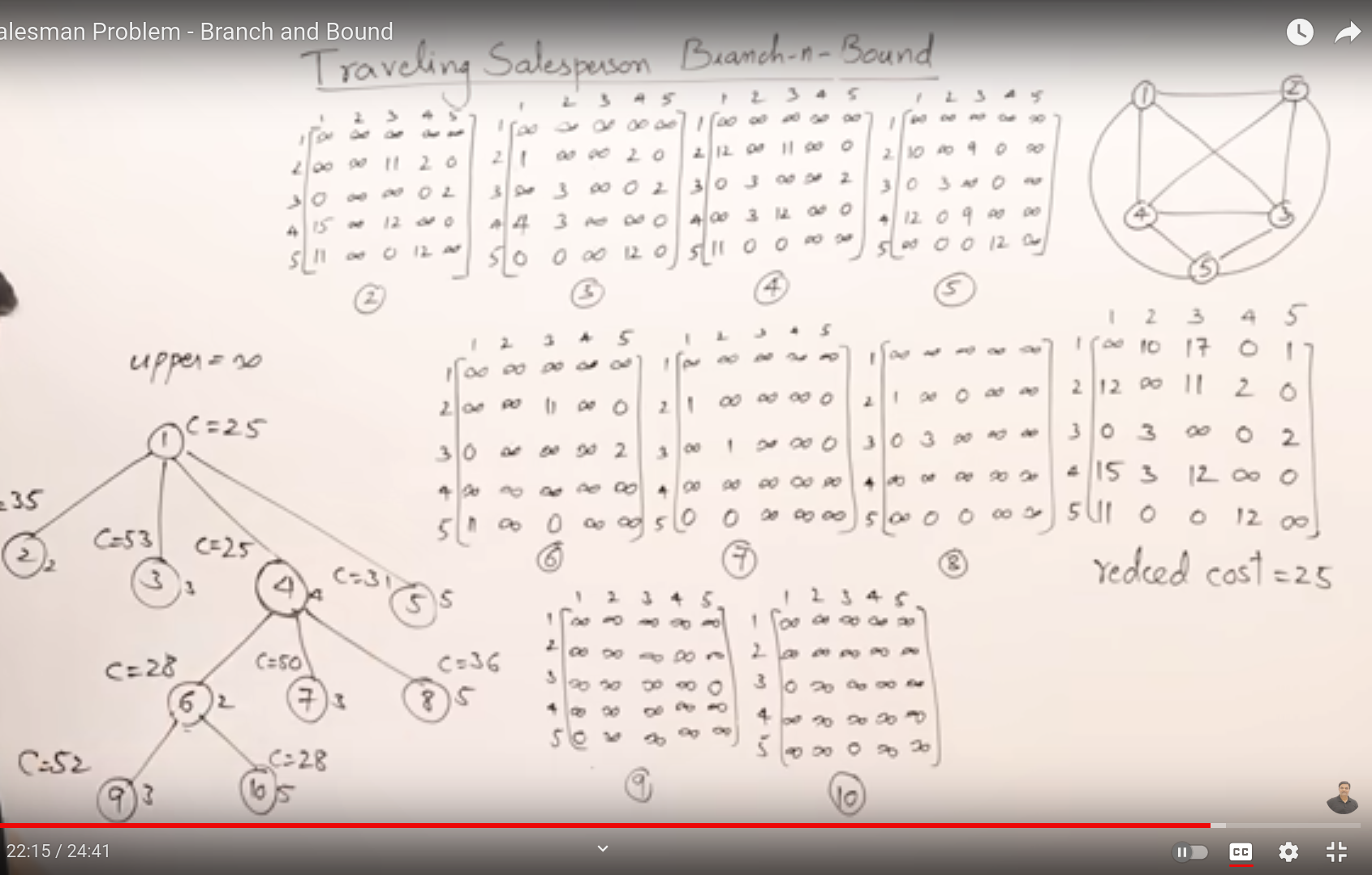
  • Quit When you have reached a leaf node and all the other costs are greater than or equal to the leaf node's cost!

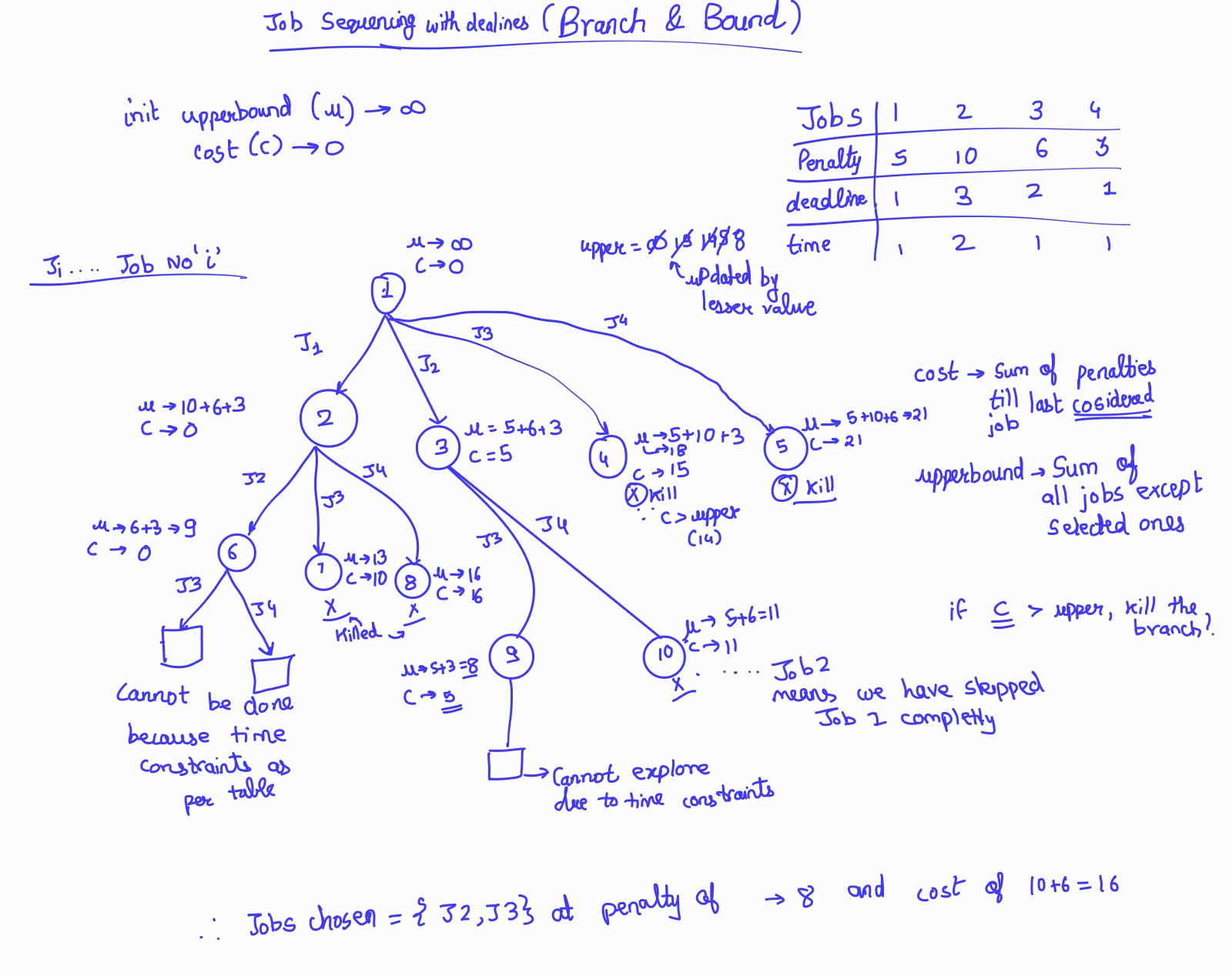
Job Sequencing with Deadlines

• Input -> 3 array of length n
  • Penalty (time)
  • deadline
  • time
• Approach by generating state space tree with cost and upper bound
  • upper bound -> sum of all penalties except that included in solution
  • cost -> sum of penalties till the last job considered
• Also make sure to tally your branch with the time parameter as some meetings cannot be scheduled after a certain time frame has passed and thus the branch also might be killed due to that