Divisors
- '\(|\)' (pipe) \(\rightarrow\) "divides"
- if \(a = b * c\), then \(b\) and \(c\) divide (are factors of) \(a\).
- This can be written as '\(b\ |\ a\ \land \ c\ | \ a\)'
- '/' (slash) \(\rightarrow\) '"divided by'
- \(a / b \rightarrow\) a divided by b
- Properties
- \(a|1\) then \(a = \pm 1\)
- \(a|b\ \&\ b|a\) then \(a=\pm b\)
- \(b/=0\) divides 0
- if b is not equal to 0 it divides zero!
- \(a|b\ and\ b|c\), then \(a|c\)
- \(b|g\ and\ b|h\) then \(b|(mg\ + \ nh)\)
- for any arbitrary numbers
- In simple words, any random numbers m,n will still result in \(b\) dividing the result.
- Even if \(m,n\) are the same i.e. \(m=n\)
Prime Numbers
- Positive integer greater than 1 having no factors other than 1 and itself is called a prime number.
- Positive integers greater than 2; that are not prime are called composite numbers.
- Any number \(n \ge 2\) is expressible as a unique product of 1 or more prime numbers.
Relative Prime Numbers
- aka co-prime numbers
- \(a,b\) are relatively prime if \(gcd(a,b) = 1\).
- \(gcd\) can be determined by comparing prime factors and selecting the least powers of the factor.
- i.e. For every factor, we choose the least powers among the factors of the two equations.
- \(gcd(24,36)\)
- \(24= 2 * 2 * 2 * 3\rightarrow2^{3}*3\)
- \(36 = 2*2*3*3\rightarrow2^{2}*3^{2}\)
- Thus \(gcd(24,36) = 2^{min(3,2)} * 3^{min(1,2)}\) = \(2^{2}*3=4*3=12\)
- PS 3,2 are the powers of 2 AND 1,2 are the powers for 3 in the factorisation respectively.
- Not necessary that both the numbers should be prime numbers
- A prime number is relatively prime to any other number
Modular Arithmetic
- Revise: MOD of a number m with base n
- If m = 23, n = 9 \(\rightarrow\) \(23 \ mod \ 9\ = 5\ mod\ 9\)
- If m = -15, n = 0 \(\rightarrow\) \(-15\ mod\ 9\ = -15+9+9 \ = 3\ mod\ 9\)
Properties
- Addition of modular number with two number \(p,\ q\) , with same modular base \(n\) is,
- \((p\ mod\ n\ + \ q\ mod\ n)\ mod\ n\ =\ (p+q)\ mod\ n\)
- Subtraction of modular number with two number \(p,\ q\) , with same modular base \(n\) is,
- \((p\ mod\ n\ - \ q\ mod\ n)\ mod\ n\ =\ (p-q)\ mod\ n\)
- Multiplication of modular number with two number \(p,\ q\) , with same modular base \(n\) is,
- \((p\ mod\ n\ * \ q\ mod\ n)\ mod\ n\ =\ (p*q)\ mod\ n\)
- \(m^{a}\ mod\ n\ = \ m^{pq}\ mod\ n\) where \(a=p*q\) \(\Rightarrow\) \((m^{p}\ mod \ n)^{q}\ mod\ n\)
- Congruence: \(a,b\) are congruent (\(a\cong b\)) if the remainder obtained after performing mod with same number \(n\) on both \(a,b\) is the same.
- Division
- \(b/a\ mod\ n\ = b*a^{-1} \ mod\ n\)
- \(a^{-1}*a = 1 \ mod \ n\)
- Inverse might not always exist, it exists when
- Additive Inverse Property:
- a + (-a) = 0
- but for mod, we have to think with respect to \(n\)
- \(a^{-1} = n - a\)
- if \(n = 12, a = 7, a^{-1} = n-a\)
- \(i.e\ 12-7\ =\ 5; a^{-1} = 5\)
- Multiplicative Inverse
- Under mod \(n\), \(a*a^{-1} \cong 1 mod n\)
- n = 11, a = 2, \(a^{-1}\) = ?; \(2*6\ mod\ 11 = 1\ mod\ 11\), Thus, \(a^{-1} = 6\)
- Multiplicative inverse only exists when \(gcd(n,a) = 1\) i.e. a,n are relatively prime.
- Another approach \(\rightarrow\) #Extended Euclidean Algorithm]
Galois Field
- Defined over prime numbers
- Denoted by \(GF(p^{n})\)
- set of integers {0, 1 .. p-1} with arithmetic operations modulo prime p
Prime Factorisation
- when a number is written as a product of primes.
Euler's Totient Function
- \(\phi(n)\) is number of positive integers less than \(n\) which are relatively prime to n

- By solving a different examples; the third formula can be extended and used with \(k\) prime numbers in a statement
- Example, \(\phi(372) \ = \ 2*2*3*31 = \phi(2^{2}) *\phi(3) * \phi(31) = (4-2)*2*30\ = \ 120\)
Fermat's theorem
- If \(p\) is prime and \(p \centernot\mid a\) then \(a^{p-1} \cong\ 1\ mod\ p\)
- generalisation: \(a^{\phi(n)} \ mod \ n = 1\), where \(gcd(a,n) = 1\)
- This is used when n is not prime number; we need a,n to be co-prime here
- Example, \(2^{63} \ mod \ 99\)
- $\(R(\frac{k*a}{k*d})=(k)R(\frac{a}{d})\)$ Where, R -> Remainder function
- \(a, a^{'}\) be integers, \(b\) be a positive integer. We say that "\(a\) is congruent to \(a^{'}\) modulo \(b\)" iff \(b\ | \ (a-a^{'})\) \(\Leftrightarrow\) (which is equivalent to) \(a\ mod\ b\ = \ a^{'}\ mod\ b\)
- a and b have the same remainder when divided by n! That's it!
- \(a = k*n + b\) ; k,a,b are integers. n is a positive integer!
- \(n \ | (a-b)\)
- For exam, remember this formula: \(b\ | (a-a^{'})\) i.e. a is congruent to a' if and only if b divides (a-a') completely.
- Addition \(\rightarrow\) (a+b) mod n ≡ (a mod n) + (b mod n)
- Subtraction \(\rightarrow\) a-b mod n ≡ a+(-b) mod n
- Multiplication \(\rightarrow\) a*b mod n; possible to get a*b ≡ 0 even though, neither a,b ≡ 0 mod n
- Division \(\rightarrow\) b/a mod n
- multiplied by inverse of a i.e. b/a \(\Leftrightarrow\) \(b*a^{-1}\ mod\ n\)
- PS \(a*a^{-1}\ =\ 1\ mod\ n\)
- e.g. \(3^{-1} ≡ 7\ mod\ 10\), since 3*7 ≡ 1 mod 10
- Inverse exists only when \(gcd(a,n) = 1\), may not always exist.
- Multiplicative inverse
- In \(Z_n\), an element \(a\) has a multiplicative inverse \(b\) if:
- \(a \times\ b \cong \ 1\ mod\ n\)
- for b to exist, a,n must be coprime
- 0 never has an inverse
- 1 is always its own inverse
- Numbers having inverses in \(Z_n\) are relatively prime to \(n\).
Euclidean Algorithm
- Find \(gcd\) of \(a,b\) such that \(a \ge b \ge 0\)
- We use the fact that, if a,b have a divisor d, then so does a-b, a-2b
- Algorithm
A=a, B=b
while B >0:
R = A mod B
A = B, B = R
Return A;
Extended Euclidean Algorithm
- For given integers and , the extended Euclidean algorithm not only calculate the greatest common divisor but also two additional integers and that satisfy the following equation.
- x and y will have opposite signs
- Book examples on page 169(145)
-
imp`.
- Algorithm
- Two positive numbers, p & q such that p >= q
- if q = 0; r = o, x1 = 1, y1 = 0
- if q > 0;
- z = p|q, r = p mod q, \(x_1 = x_3-zx_2\), $ <<>$
Multiplicative Inverse using GF field
multiplicative inverse using GF hot (m,b):
Q,A1,A2,A3,B1,B2,B3,T1,T2,T3;
Init(): A1 = 1, A2 = 0; B1 = 0, B2 = 1;
A3 = m > b ? m : b; // greater one
B3 = m < b ? m : b; // smaller one
while B3 > 0:
Ti = Ai - Q*Bi;
Ai = Bi; Bi = Ti;
Primitive Root
- a is a primitive root of prime number \(p\) if \(a^{i}\ mod\ p\) gives distinct values for \(i \le p-1\)
- Example: Is 2 a primitive root of prime number 5?
- 2^1 mod 5 = 2;
- 2^2 mod 5 = 4;
- 2^3 mod 5 = 3;
- 2^4 mod 5 = 1;
- Thus the above remainder values are all distinct. Thus 2 is a primitive root of 5.
- if n is a non prime number, \(Z_n^{x}\) is the congruence classes that might contain primitive root, so we try them for primitive root.
- For Example, \(\phi(14) = 6\)
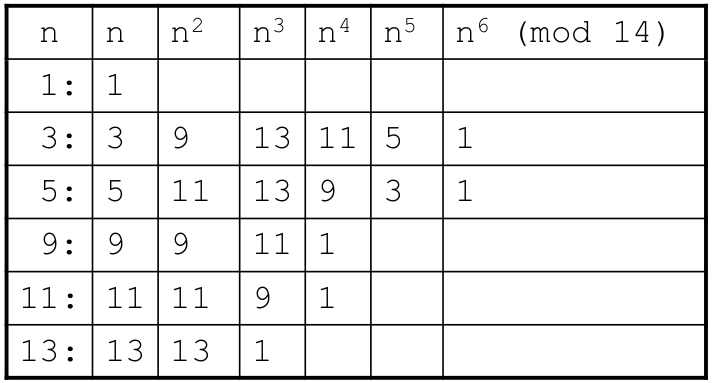
- Here, 3 & 5 are primitive roots mod 14.
Discrete Logarithm
- \(a^{x} = b\ mod\ p\) can have multiple values for \(x\).
- There is no way to find a sure value for x used originally, as there might be multiple values.
- Exponentiation, finding a value when x is given, is relatively easy, but finding discrete logarithms is a hard problem
Chinese Remainder Theorem:
- $\(X=(a_1M_1M_1^{-1} + a_2M_2M_2^{-1} ... + a_nM_nM_n^{-1} )\ mod\ M\)$where,
- M is the product of all modulo values i.e. \(m_1*m_2...*m_n\)
- \(M_i = \frac{M}{m_i}\)
- \(M_i*M_i^{-1} =\ 1 \ mod\ m_i\) // calculate inverse value here.

