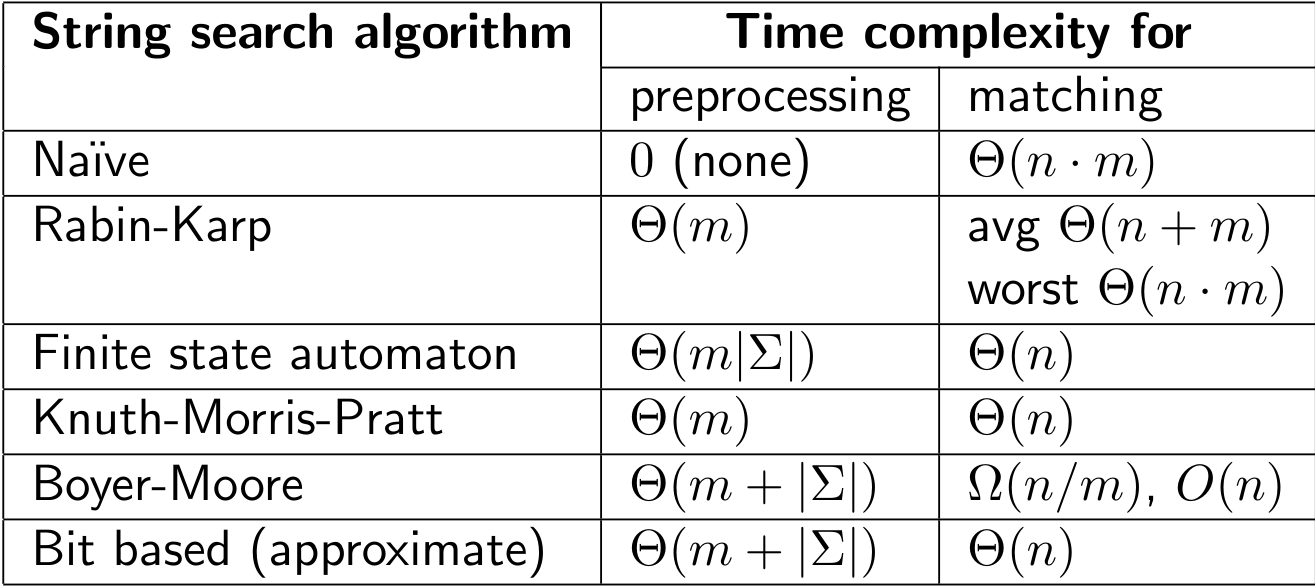
String Matching

  • Find one, or more, generally all the occurrences of a pattern x in a text string.
  • Two variants
    1. Given a pattern, find occurrences in any initially unknown text
      • preprocess the pattern using Finite automata models or combinatoric properties of strings
    2. Given a text, find occurrences of any initially unknown pattern
      • Solutions by indexing the text with the help of trees or finite automata stringSearchTimeComplexity.png

Naive (BruteForce) Algo 

for ( i = 0; i <= n - m; i++ ) {
    for ( j = 0; j < m && x[j] == y[i + j]; j++ );
    if ( j >= m ) return i;
}
- Time Complexity -> O(mn)

Knuth-Morris-Pratt Algorithm - Given a pattern, we have to find a prefix and suffix of a pattern - observation: after a mismatch, the word itself allows us to determine where to begin the next match to bypass re-examination of previously matched characters - Prepare a prefix table | 1 | 2 | 3 | 4 | 5 | | a | b | a | b | d | | 0 | 0 | 1 | 2 | 0 |
- Preparing PI table -> m time - searching through the string -> n time - T.C. -> O(n + m) - At most 2n − 1 character comparisons during the text scan - Feynman term explanation - You iterate through the string character by character if you find matches in pattern you go ahead in the pi table's pattern. If a character does not match you go to the previous index of the current character's pi value in J.

Rabin-Karp Algorithm - Downside -> Spurious Hits cause time complexity to go to O(mn) in worst case if a simple hash function is used - a->1,b->2,c->3,d->4,e->5,f->6,g->7,h->8,i->9,j->10 --- This function if used directly has a chance of causing spurious hits - for a pattern of size m, we can have\(\(a*10^{m-1} + b*10^{m-2} + c*10^{m-3} ...\)\) - When the window slides, subtract \(a*10^{m-1}\), multiply the remaining answer by 10 (so that we increase the powers of the internal parts by 10) and then lastly add the next element to it (\(d*10^{0}\)) - After the optimal algorithm is applied -> \(\theta(n-m+1)\) - Worst Case -> O(nm) - If the hash value is too big you might apply a MOD to the function depending on the size, language, etc. but applying MOD may also result in spurious hits! - We create a hash value for the pattern and compare it with the current window of the same size of the text

Boyer-Moore Algorithm: - "best practical choice” algorithm - Learn from character comparisons to skip pointless alignment - Try alignment in right-to-left order - Bad character rule -> Upon mismatch, skip alignments until (occurrence shift) - Mismatch becomes a match - P moves past mismatched character - Good suffix rule -> Substring matched by inner loop; skip until (matching shift) - there are no mismatches between P and t - P moves past t - Worst Case complexity -> O(m+n) - Best Case -> O(n/m)BoyerMooreGoodSuffixRule.png